概论

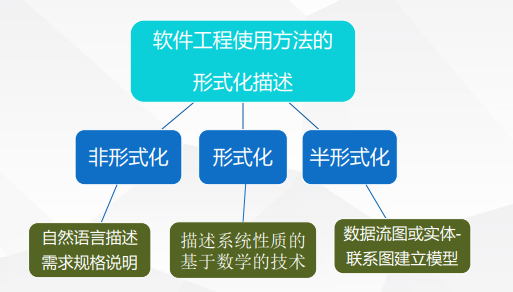
用自然语言书写的系统规格说明书，可能存在矛盾、二义性、含糊性、不完整性及抽象层次混乱等问题。

为了克服非形式化方法的缺点，人们把数学引入软件开发过程，创造了基于数学的形式化方法。

结构化方法的分析结果由以下几部分组成：一套分层的数据流图、一本数据词典、一组小说明(也称加工逻辑说明)、补充材料。

• 基于模型的方法

  • 通过明确定义状态和操作来建立一个系统模型（使系统从一个状态转换到另一个状态）
  • 可以表示非功能性需求（诸如时间需求）， 但不能很好地表示并发性
  • Z语言

• 基于逻辑的方法

  • 用逻辑描述系统预期的性能，包括底层规约、时序和可能性行为

• 过程代数方法

  • 通过限制所有容许的可观察的过程间通信来表示系统行为,允许并发过程表示
  • 通信顺序过程（CSP）

• 基于网络的方法

  • 图形化表示法易于理解
  • 一种通用的系统确定表示法
  • 采用具有形式语义的图形语言，为系统开发和再工程带来特殊的好处
  • Petri图，计时Petri图，状态图

有穷状态机

• 一个有穷状态机可以表示为一个5元组(J，K，T，S，F)， 其中：

  • J是一个有穷的非空状态集；

  • K是一个有穷的非空输入(事件)集；

  • T是一个从(J-F)×K到J的转换函数；

  • S∈J，是一个初始状态；

  • F∈J，是终态集。

• 有穷状态机方法采用了一种简单的格式来描述规格说明： 当前状态+事件+谓词=>下个状态

• 谓词是一个状态，形式化方法允许把事件和状态作为谓词对待。

• 这种形式的规格说明易于书写、易于验证，而且可以比较容易地把它转变成设计或程序代码。

• 可以开发一个CASE工具把一个有穷状态机规格说明直接转变为源代 码

• 和数据流图方法一样，形式化的有穷状态机方法也没有处理定时需求

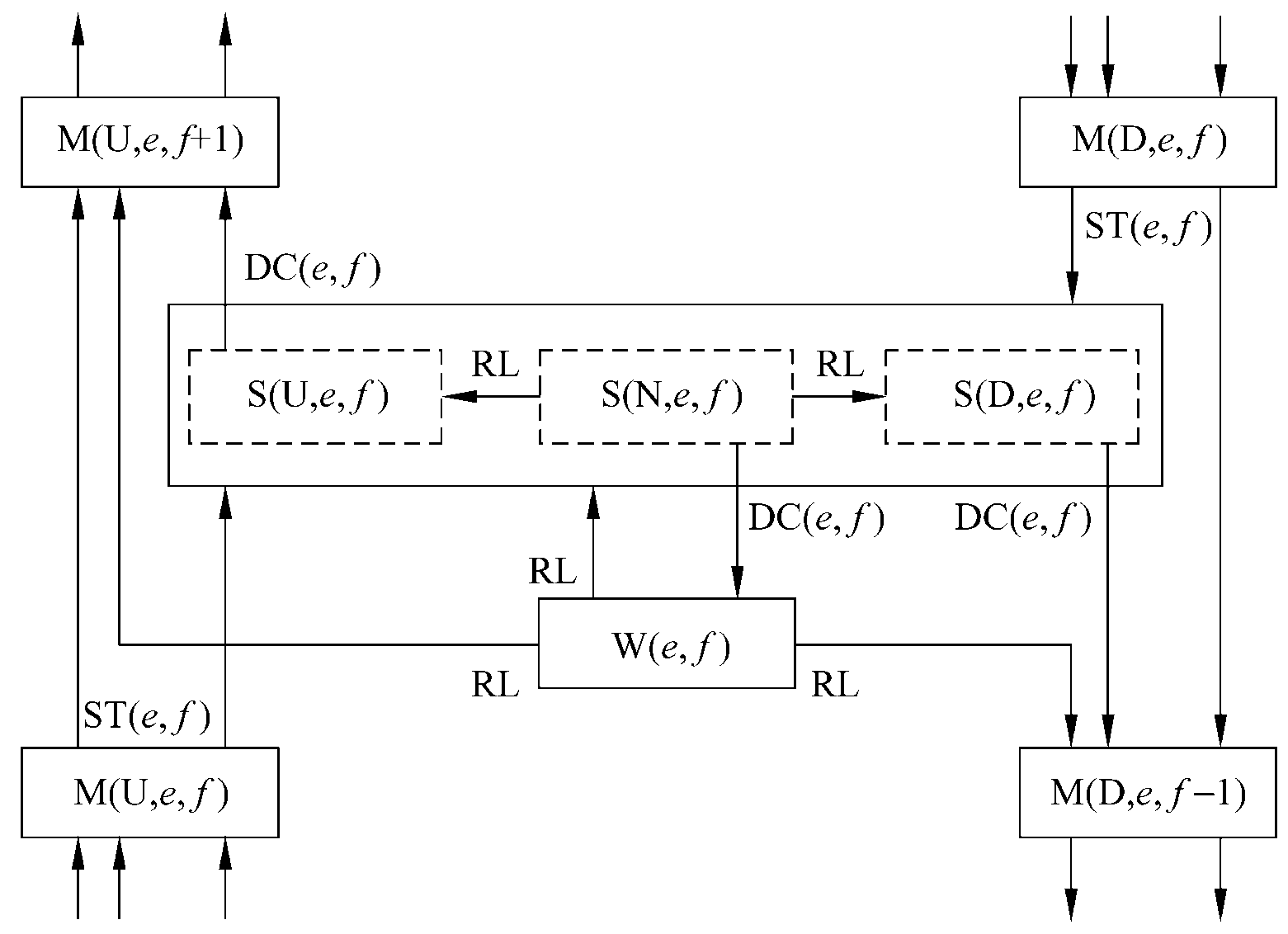
☆Petri网

Petri网包含4种元素：一组位置P、一组转换T、输入函数I以及输出函数O

并发系统中遇到的一个主要问题是定时问题。这个问题可以表现为多种形式，如同步问题、竞争条件以及死锁问题。 用于确定系统中隐含的定时问题的一种有效技术是Petri网

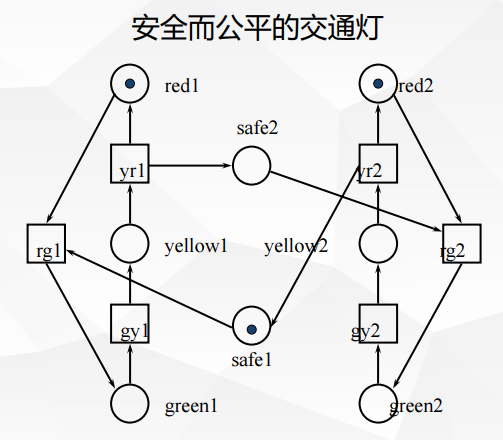
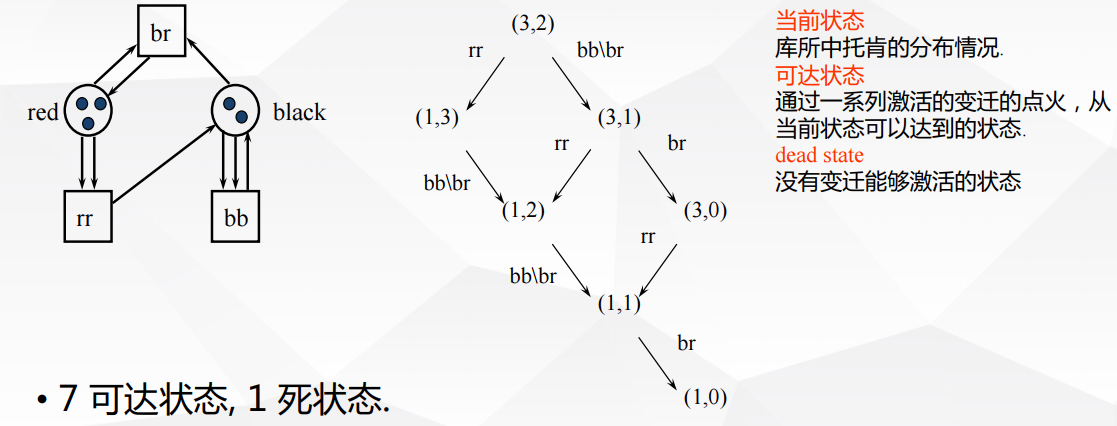
• Petri网是一个由places 和transitions构成的网络

• 如果输入places都包含了token，那么transitions就被激活

• Petri网具有非确定性，如果数个转换都达到了激发条件，则其中任意一个都可以被激发

• Petri网的一个重要扩充是加入禁止线。禁止线是用一个小圆圈而不是用箭头标记的输人线。

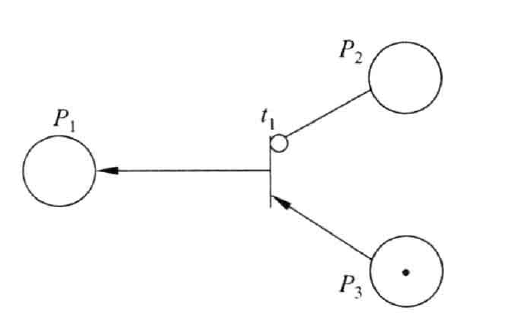
  • 通常，当每个输入线上至少有一个权标，且禁止线上没有权标的时候，相应的转换才是允许的。

Z语言

Z语言是目前使用最广泛的一种形式化描述语言，在软件产业的一些大型项目中已经获得成功的应用

• 给定的集合、数据类型及常数
• 状态定义
• 初始状态
• 操作